Формула закона Ома
В данной статье расскажем про закон Ома, формулы для полной цепи (замкнутой), участка цепи, неоднородного участка цепи, в дифференциальной и интегральной форме, переменного тока, а также для магнитной цепи. Вы узнаете какие материалы соответствуют и не соответствуют закону Ома, а также где он встречается.
Закон Ома: постоянный ток  , протекающий через проводник, прямо пропорционален напряжению
, протекающий через проводник, прямо пропорционален напряжению  , приложенному к его концам и обратно пропорционален сопротивлению
, приложенному к его концам и обратно пропорционален сопротивлению  .
.
Закон Ома был сформулирован немецким физиком и математиком Георгом Омом в 1825-26 годах на основе опыта. Это экспериментальный закон, а не универсальный — он применим к некоторым материалам и условиям.
Закон Ома является частным случаем более позднего и более общего — второго закона Кирхгофа
Ниже будет представлено видео, в котором объясняется закон Ома на пальцах.


Формула закона Ома для участка цепи
Интенсивность постоянного тока, протекающего через проводник, пропорциональна напряжению, приложенному к его концам. В интернете часто называют данную формулу первым законом Ома:

I — сила (интенсивность) тока
Электрическое сопротивление:
Коэффициент пропорциональности R называется электрическим сопротивлением или сопротивлением.
Отношение напряжения к току для данного проводника является постоянным:

Единица электрического сопротивления составляет 1 Ом (1 Ω):

Резистор имеет сопротивление 1, если приложенное напряжение 1 вольт и сила тока составляет 1 ампер.
Зависимость электрического сопротивления от размера направляющей:
Сопротивление проводящей секции с постоянным поперечным сечением R прямо пропорционально длине этого сегмента li, обратно пропорциональному площади поперечного сечения S:

R — электрическое сопротивление
ρ — удельное сопротивление
I — длина направляющей
S — площадь поперечного сечения
Эта зависимость была подтверждена экспериментально британским физиком Хамфри Ди в 1822 году до разработки закона Ома.
Закон Ома для замкнутой (полной) цепи

Закон Ома для полной цепи — это значение силы (интенсивности) тока в настоящей цепи, который зависит от сопротивления нагрузки и от источника тока (E), также его называют вторым законом Ома.
Электрическая лампочка является потребителем источника тока, подключив их вместе, они создают полную электро-цепь. На картинке выше, вы можете увидеть полную электрическую цепь, состоящую из аккумулятора и лампы накаливания.
Электричество, проходит через лампу накаливания и через сам аккумулятор. Следовательно, ток проходя через лампу, в дальнейшем пройдет и через аккумулятор, то есть сопротивление лампочки складывается со сопротивлением аккумулятора.
Сопротивление нагрузки (лампочка), называют внешним сопротивлением, а сопротивление источника тока (аккумулятора) — внутренним сопротивление. Сопротивление аккумулятора обозначается латинской буквой r.
Когда электричество течет вокруг цепи, внутреннее сопротивление самой ячейки сопротивляется потоку тока, и поэтому тепловая энергия теряется в самой ячейке.

- E = электродвижущая сила в вольтах, V
- I = ток в амперах, A
- R = сопротивление нагрузки в цепи в Омах, Ω
- r = внутреннее сопротивление ячейки в Омах, Ω
Мы можем изменить это уравнение;


В этом уравнении появляется ( V ), что является конечной разностью потенциалов, измеренной в вольтах (V). Это разность потенциалов на клеммах ячейки при протекании тока в цепи, она всегда меньше э.д.с. ячейки.
Закон Ома для неоднородного участка цепи



Если на участке цепи действуют только потенциальные силы (Рисунок 1а), то закон Ома записывается в известном виде  . Если же в кругу проявляется еще и действие сторонних сил (Рисунок 2б), то закон Ома примет вид
. Если же в кругу проявляется еще и действие сторонних сил (Рисунок 2б), то закон Ома примет вид  , откуда
, откуда  . Это и есть закон Ома для любого участка цепи.
. Это и есть закон Ома для любого участка цепи.
Закон Ома можно распространить и на весь круг. Соединив точки 2 и 1 (Рисунок 3в), преобразуем разность потенциалов в ноль, и учитывая сопротивление источника тока, закон Ома примет вид  . Это и есть выражение закона Ома для полной цепи.
. Это и есть выражение закона Ома для полной цепи.
Последнее выражение можно представить в различных формах. Как известно, напряжение на внешнем участке зависит от нагрузки, то есть  или
или  , или
, или  .
.
В этих выражениях Ir — это падение напряжения внутри источника тока, а также видно, что напряжение U меньше ε на величину Ir . Причем, чем больше внешнее сопротивление по сравнению с внутренним, тем больше U приближается к ε.
Рассмотрим два особых случая, в отношении внешнего сопротивления цепи.
1) R = 0 — такое явление называют коротким замыканием. Тогда, из закона Ома имеем —  , то есть ток в цепи возрастает до максимума, а внешний спад напряжения U → 0. При этом в источнике выделяется большая мощность, что может привести к его неисправности.
, то есть ток в цепи возрастает до максимума, а внешний спад напряжения U → 0. При этом в источнике выделяется большая мощность, что может привести к его неисправности.
2) R = ∞ , то есть электрическая цепь разорвана, тогда  , а
, а  . Итак, в этом случае, ЭДС численно равна напряжению на клеммах разомкнутого источника тока.
. Итак, в этом случае, ЭДС численно равна напряжению на клеммах разомкнутого источника тока.
Закон Ома в дифференциальной форме
Закон Ома можно представить в таком виде, чтобы он не был связан с размерами проводника. Выделим участок проводника Δ l , на концах которой приложено потенциалы φ 1 и φ 2. Когда средняя площадь сечения проводника Δ S , а плотность тока j , то сила тока 
Если Δ l → 0, то взяв предел отношения,  . Итак, окончательно получим
. Итак, окончательно получим  , или в векторной форме
, или в векторной форме  — это выражение закона Ома в дифференциальной форме. Этот закон выражает силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.
— это выражение закона Ома в дифференциальной форме. Этот закон выражает силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.
Закон ома для переменного тока

Это уравнение представляет собой запись закона Ома для цепей переменного тока относительно их амплитудных значений. Понятно, что оно будет справедливым и для эффективных значений силы и тока:  .
.
Для цепей переменного тока возможен случай, когда  , а это значит, что U L = U C . Поскольку эти напряжения находятся в противофазе, то они компенсируют друг друга. Такие условия называют резонансом напряжений. Резонанс можно достичь или при ω = const , изменяя С и L , или же при постоянных С и L подбирают ω, которая называется резонансным. Как видно —
, а это значит, что U L = U C . Поскольку эти напряжения находятся в противофазе, то они компенсируют друг друга. Такие условия называют резонансом напряжений. Резонанс можно достичь или при ω = const , изменяя С и L , или же при постоянных С и L подбирают ω, которая называется резонансным. Как видно —  .
.
Особенности резонанса напряжений следующие:
- полное сопротивление цепи минимальное, Z=R ;
- амплитуда тока — максимальная
 ;
; - амплитуда значений приложенного напряжения равна амплитуде на активном сопротивлении;
- напряжение и ток находятся в одинаковых фазах (φ = 0);
- мощность источника передается только активному сопротивлению, следовательно полезная мощность — максимальная.

Резонанс токов получают при параллельном соединении индуктивности и емкости на рисунке слева. По первому закону Кирхгофа результирующий ток в какой-то момент времени I = IL+IC. Несмотря на то, что суммы ІL и IC могут быть достаточно большими, ток в главном круге станет равным нулю, а значит сопротивление цепи станет максимальным.
Зависимость силы тока от частоты при различных активных сопротивлениях показана на рисунке справа.
Закон Ома в интегральной форме
С дифференциального закона Ома можно непосредственно получить интегральный закон. Для этого умножим скалярно левую и правую части выражения  на элементарную длину проводника
на элементарную длину проводника  (перемещение носителя тока), образовав соотношение
(перемещение носителя тока), образовав соотношение

В (1) j*S n = И есть величина силы тока. Проинтегрируем (1) по участку круга L с точки 1 до точки 2
есть сопротивление проводника, а  — удельное сопротивление. Интеграл в правой части (2) является напряжение U на концах участка
— удельное сопротивление. Интеграл в правой части (2) является напряжение U на концах участка
Окончательно из (2) — (4) имеем выражение для закона Ома в интегральной форме
который он установил экспериментально.
Интерпретация закона Ома
Интенсивность тока, являющаяся действием приложенного напряжения, ведет себя пропорционально его напряжению. Например: если приложенное напряжение увеличивается в два раза, оно также удваивает силу тока (интенсивность тока).
Помните, что закон Ома удовлетворяется только частью материалов — в основном металлами и керамическими материалами.
Когда закон Ома встречается и какие материалы соответствуют и не соответствуют закону Ома
Закон Ома является экспериментальным законом, выполненным для некоторых материалов (например, металлов) для фиксированных условий тока, в частности температуры проводника.
Материалы, относящиеся к закону Ома, называются омическими направляющими или линейными проводниками. Примерами проводников, которые соответствуют закону Ома, являются металлы (например, медь, золото, железо), некоторые керамические изделия и электролиты.
Материалы, не относящиеся к закону Ома, в которых сопротивление является функцией интенсивности протекающего через них тока, называются нелинейными проводниками. Примерами руководств, не относящихся к закону Ома, являются полупроводники и газы.
Закон Ома не выполняется, когда изменяются параметры проводника, особенно температура.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Формулировка и определение закона Ома
Закон Ома для всей цепи является одним из наиболее фундаментальных и важных законов, регулирующих работу электрических и электронных схем. Он описывает взаимоотношение тока, напряжения и сопротивления для линейного участка цепи, так что если два известны, третий может быть получен расчетным путем.
Закон Ома — основа электротехники
Это основное уравнение, используемое для изучения электрических цепей, было получено экспериментальным путем Георгом Симоном Омом. Он родился в Эрлангене Германии в 1787 году и поступил в университет этого города в 1805 году, где он получил докторскую степень. Георг преподавал математику в школах и проводил эксперименты по физике в школьной физической лаборатории, пытаясь понять принципы электромагнетизма.

В 1827 году он опубликовал статьи, в которых описана математическая модель того, как контуры проводят тепло в работах Фурье. Ом получил экспериментальные данные, на базе которых впервые смог сформулировать свой закон 8 января 1826 года. Он установил, что разность потенциалов между двумя точками в цепи равна произведению тока между ними на общее сопротивление всех электрических устройств. Чем больше напряжение батареи или ее общая разность электропотенциалов, тем больше будет ее ток. Аналогично, с большим сопротивлением он будет меньше.
Но его исследования не нашли должного понимания и Георг оставил свою работу в Кельне. Только в 1833 году он получил должность профессора в Нюрнберге. Выводы Ома послужили катализатором для новейших исследований по электричеству. В 1841 году ученого наградили медалью Копли, а в 1872 году «Ом» был принят в качестве единицы сопротивления в электрических цепях.
Закон Ома для полной электрической цепи описывает протекание тока через проводящие металлы, когда применяются различные уровни напряжения. Некоторые материалы, такие как электропровода, имеют небольшое сопротивление току — этот тип материала называется проводником.
Важно! В других случаях материал может препятствовать протеканию тока, но, тем не менее, допускает его использование. В электрических цепях эти компоненты часто называют резисторами. Существуют материалы, которые практически не пропускают ток, они называются изоляторами.
Формула закона Ома
Первый Закон Ома устанавливает, что разница потенциалов между двумя точками резистора пропорциональна току. Более того, согласно этому закону, соотношение между потенциалом и током всегда является постоянным для омических резисторов.
V — напряжение/электропотенциал (В);
R — электросопротивление (ом);
I — электрический ток.

В нем U является скалярной величиной и меряется в (В). Разница в электропотенциалах между двумя точками цепи, указывает на наличие электросопротивления. Когда I проходит через резистивный элемент R, происходит падение электрического потенциала. Это различие возникает из-за рассеивания энергии, называемым эффектом Джоуля. I измеряет поток зарядов через тело в (А) и прямо пропорционален сопротивлению провода.
Второй закон Ома говорит о том, что электросопротивление R представляет собой свойство из тела, которое регулирует проходимость I. Это свойство зависит от геометрических факторов тела, таких как длина или площадь сечения участка и от вызываемой величины R. Его количество зависит исключительно от материала участка.
R — электросопротивление (Ом);
ρ — удельное электросопротивление провода (Ом.м);
L — протяженность проводника (м);
S — площадь сечения провода (м2).
Омическим резистором называется любое тело, способное представлять постоянное сопротивление для данного диапазона напряжений. График напряжения как функция тока для омических резисторов является линейным. Резистор можно считать омическим в диапазоне, в котором его потенциал линейно возрастает с ростом I.
Сопротивление можно понимать как наклон линии, заданный тангенсом угла. Как известно, тангенс определяется, как отношение между противоположным и соседним сторонами, и, в случае, когда сопротивления омические, может быть рассчитан по формуле: R = U / I.

Чтобы помочь запомнить формулу, можно использовать треугольник с одной горизонтальной стороной и вершиной вверху, как пирамиду. Это иногда называют законом треугольника Ома. В верхнем его углу находится буква V, в левом углу — буква I, а в правом нижнем углу — R.
Обратите внимание! Чтобы использовать треугольник, прикрыть неизвестный параметр, а затем, рассчитать его из двух других. Если они находятся на одной линии, они умножаются, но если одна находится над другой, их следует разделить. Другими словами, если необходимо рассчитать I, напряжение делится на сопротивление, то есть V / R.
Для полной замкнутой цепи
Закон Ома для полной цепи определение — ЭДС электрического элемента аккумулятора или источника — это общая работа, выполненная внутри и снаружи элемента для переноса электрических зарядов в электроцепи. Если обозначим ЭДС аккумулятора через E (B), суммарная сила тока для полной цепи I (А), внешнее сопротивление R (Ом) и внутреннее сопротивление ячейки r по (Ом).
Тогда: E = I*R + I*r

Это выражение известно, как закон Ома для замкнутого контура, где: I — интенсивность тока равна E общей электродвижущей силе деленной на (R + r) — общее сопротивление цепи.
Связь между ЭДС (E) электрической ячейки и напряжением на ее полюсах (V). На основании закона Ома для замкнутых цепей:
E = IR + I r, V = IR
ЭДС электрической ячейки больше, чем разность потенциалов между клеммами ее внешней цепи, когда цепь включена. Потому что внутреннее сопротивление ячейки потребляет работу для передачи I внутрь нее на основе соотношения E = V + I r и, следовательно, V Для участка цепи
Законы Ома для участка цепи применяются также часто, как и для замкнутого контура. Разница в том, что при расчете учитывается не ЭДС, а только разность потенциалов. Такой участок называется однородным. В этом случае существует особый случай, который позволяет рассчитать характеристики электрической цепи на каждом из ее элементов.

V — разность напряжений или потенциалов. Измеряется вольтметром при параллельном подключении щупов к клеммам любого элемента (сопротивления). Результирующее значение V всегда меньше, чем ЭДС.
Для переменного тока
Общим термином для сопротивления переменного I является полное сопротивление и обозначается символом Z. Треугольник используется точно также, как закон Ома в DC, за исключением того, что теперь используют сопротивление Z. Следует отметить, что при измерении переменного напряжения или тока измеритель будет показывать только правильные значения в ограниченном диапазоне частот. Обычно это справедливо для постоянного I до 400 Гц.

Для цепей переменного тока, в которых напряжение и I находятся в фазе, может использоваться круговая диаграмма. В случае цепей переменного тока напряжение связано с I с помощью константы пропорциональности Z (импеданса) и константы пропорциональности R для чисто резистивных цепей, где (Z = R).
V = IZ и V = IR (для чисто резистивных цепей)
Где Z = √ [R 2 + X 2]
Импеданс Z — это полное сопротивление цепей к переменному току. Он состоит из реальной части (сопротивления) и мнимой части (реактивности).
В интегральной форме
Наиболее часто в электротехнике используют омическое соотношение в интегральной форме. Если рассмотреть часть проводника, приняв для простоты, что он имеет цилиндрическую форму, с площадью поперечного сечения S, к концам которого приложена разность потенциалов Δ φ = φ 1- φ 2, то внутри проводника будет действовать электрополе с плотностью тока j = σ*Е в соответствии с Законом Ома. Если предположить, что I будет равномерен по площади сечения провода, тогда:

Если поле Е в проводнике однородно, вектор Е будет направляться вдоль оси Ох, в этом случае напряжённость поля будет взаимосвязана с потенциалом формулой
I = σ*S*dφ/dx, поэтому
Интегрируя данное выражение для всего участка провода, получится:
I* ∫ dx/dφ = φ1 — φ2
Выражение, стоящее в левой части является сопротивлением проводника R, таким образом интегральная форма Закона Ома:
I *R = φ1, φ2 = V , где:
Для проводника с формой цилиндра, где S постоянная величина R = L/(σ *S) = ρ* L/S,
где L — длина проводника, а ρ = 1/σ — удельное сопротивление.
Неоднородного участка цепи
Однако существуют компоненты электрических цепей, которые не подчиняются закону Ома, то есть их взаимосвязь между током и напряжением является нелинейной или неомической. Например, pn-переходный диод. В нем I не увеличивается линейно с приложенным напряжением для диода. Можно определить значение тока (I) для данного значения приложенного напряжения (V) по кривой, но не по закону Ома, поскольку значение «сопротивления» не является постоянной величиной.

Кроме того, I значительно увеличивается, только если приложенное напряжение положительное, а не отрицательное. Соотношение V/I для некоторой точки вдоль нелинейной кривой иногда называют статическим, хордовым или постоянным сопротивлением. Значение общего V над общим I изменяется в зависимости от конкретной точки вдоль нелинейной кривой.
Это означает, что «сопротивление постоянному току» V/I в некоторой точке кривой не совпадает с тем, которое было бы определено путем подачи переменного сигнала, имеющего пиковую амплитуду V вольт или I ампер с центром в той же точке вдоль кривой. Однако в некоторых применениях с диодами сигнал переменного тока, подаваемый на устройство, мал, и можно анализировать схему с точки зрения динамики, мало сигнальное, или инкрементное сопротивления, определяемое как сопротивление наклона кривой V-I при среднем значении напряжения. Для достаточно малых сигналов динамическое сопротивление позволяет рассчитать закон малого сопротивления Ома как приблизительно одно по наклону линии, проведенной по касательной к кривой в рабочей точке постоянного тока.
Закон Ома для участка сети однородного характера был изложен выше. Закон на нелинейном участке будет иметь следующий вид:
I = U/ R = φ1 — φ2 + E/ R, где:
φ1 — φ2 — разница потенциалов на конечных точках рассматриваемого участка сети,
R — общее сопротивление нелинейного участка цепи.
Сила тока по закону Ома
Альтернативные утверждения закона Ома заключаются в том, что I в проводнике равен разности потенциалов V на проводнике, деленной на сопротивление проводника, или просто I = V / R, и что разность потенциалов на проводнике равна произведению тока в проводнике и его сопротивления, V = IR.
В цепи, в которой разность потенциалов или напряжение постоянны, I может быть уменьшен, путем добавления большего сопротивления или увеличен путем удаления некоторого сопротивления. Закон Ома также может быть выражен в терминах электродвижущая сила, или напряжение, E — источника электрической энергии, такой как батарея, например, I = Е / R.
С изменениями закон Ома также применяется к цепям переменного тока, в которых соотношение между напряжением и током более сложное, чем для постоянных I. Именно потому, что I меняется, возникают другие формы замыкания тока, называемые реактивным сопротивлением. Сочетание сопротивления и реактивного сопротивления называется импеданс, Z. Когда импеданс, эквивалентный отношению напряжения к току, в цепи переменного тока является постоянным, обычное явление, применим закон Ома, например, V/I = Z.
Закон Ома используется во всех отраслях электротехники для расчета значения резисторов, требуемых в цепях, и также может использоваться для определения тока, протекающего в цепи, где напряжение можно легко измерить через известный резистор. Таким образом, он применяется в огромном количестве вычислений во всех формах электрических и электронных схем — фактически везде, где течет ток.
Закон Ома для участка цепи простым языком
Вся прикладная электротехника базируется на одном догмате — это закон Ома для участка цепи. Без понимания принципа этого закона невозможно приступать к практике, поскольку это приводит к многочисленным ошибкам. Имеет смысл освежить эти знания, в статье мы напомним трактовку закона, составленного Омом, для однородного и неоднородного участка и полной цепи.
 Диаграмма, упрощающая запоминание
Диаграмма, упрощающая запоминание
Классическая формулировка
Этот простой вариант трактовки, известный нам со школы.
 Однородный открытый участок электроцепи
Однородный открытый участок электроцепи
Формула в интегральной форме будет иметь следующий вид:
 Формула в интегральной форме
Формула в интегральной форме
То есть, поднимая напряжение, мы тем самым увеличиваем ток. В то время, как увеличение такого параметра, как «R», ведет к снижению «I». Естественно, что на рисунке сопротивление цепи показано одним элементом, хотя это может быть последовательное, параллельное (вплоть до произвольного)соединение нескольких проводников.
В дифференциальной форме закон мы приводить не будем, поскольку в таком виде он применяется, как правило, только в физике.
Принятые единицы измерения
Необходимо учитывать, что все расчеты должны проводиться в следующих единицах измерения:
- напряжение – в вольтах;
- ток в амперах
- сопротивление в омах.
Если вам встречаются другие величины, то их необходимо будет перевести к общепринятым.
Формулировка для полной цепи
Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.
 Схема с подключенным с источником
Схема с подключенным с источником
Учитывая «r» ЭДС, формула предстанет в следующем виде:

Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.
Напряжение будет меньше ЭДС, определить его можно по формуле:

Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.
Неоднородный участок цепи постоянного тока
Под таким типом подразумевается участок, где помимо электрического заряда производится воздействие других сил. Изображение такого участка показано на рисунке ниже.
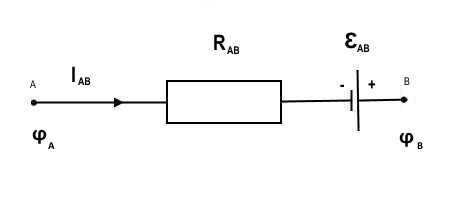 Схема неоднородного участка
Схема неоднородного участка
Формула для такого участка (обобщенный закон) будет иметь следующий вид:
 Формула для неоднородного участка цепи
Формула для неоднородного участка цепи
Переменный ток
Если в схема, подключенная к переменному току снабжена емкостью и/или индуктивностью (катушкой), расчет производится с учетом величин их реактивных сопротивлений. Упрощенный вид закона будет выглядеть следующим образом:
Где «Z» представляет собой импеданс, это комплексная величина, состоящая из активного (R) и пассивного (Х) сопротивлений.
Практическое использование
Видео: Закон Ома для участка цепи — практика расчета цепей.
Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.
 Применяем закон к любому участку цепи
Применяем закон к любому участку цепи
Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.
Находим силу тока
Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:
- Напряжение – 220 В;
- R нити накала – 500 Ом.
Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.
Рассмотрим еще одну задачу со следующими условиями:
В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА).
Вычисление напряжения
Для решения мы также воспользуемся законом, составленным Омом. Итак задача:
Преобразуем исходные данные:
Решение: 20000 Ом х 0,01 А = 200 В.
Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.
Сопротивление.
Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.
Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим.
Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».
Рассмотрим несколько примеров.
Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.
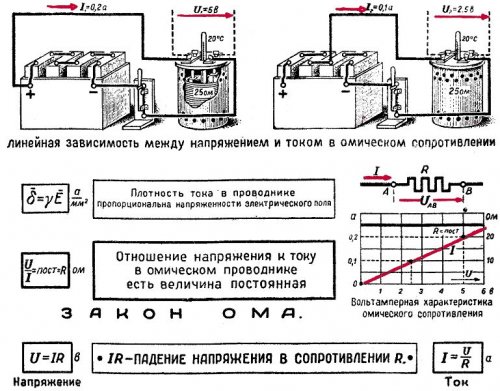
Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).
Изображение вольт-амперной характеристики, где R=1 Ом
 Изображение вольт-амперной характеристики
Изображение вольт-амперной характеристики
Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).
Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении. Там где допускается обратное направление, график будет продолжен на отрицательные значения.
Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.
Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.
Вывод
Как уже упоминалось в начале статьи, вся прикладная электротехника базируется на законе, составленном Омом. Незнание этого базового догмата может привести к неправильному расчету, который, в свою очередь, станет причиной аварии.
Подготовка электриков как специалистов начинается с изучения теоретических основ электротехники. И первое, что они должны запомнить – это закон составленный Омом, поскольку на его основе производятся практически все расчеты параметров электрических цепей различного назначения.
Понимание основного закона электротехники поможет лучше разбираться в работе электрооборудования и его основных компонентов. Это положительно отразится на техническом обслуживании в процессе эксплуатации.
Самостоятельная проверка, разработка, а также опытное изучение узлов оборудования – все это существенно упрощается, если использовать закон Ома для участка цепи. При этом не требуется проводить всех измерений, достаточно снять некоторые параметры и, проведя несложные расчеты, получить необходимые значения.
Закон Ома для участка цепи
Основным законом электротехники, при помощи которого можно изучать и рассчитывать электрические цепи, является закон Ома, устанавливающий соотношение между током, напряжением и сопротивлением. Необходимо отчетливо понимать его сущность и уметь правильно пользоваться им при решении практических задач. Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.
Закон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Если увеличить в несколько раз напряжение, действующее в электрической цепи, то ток в этой цепи увеличится во столько же раз. А если увеличить в несколько раз сопротивление цепи, то ток во столько же раз уменьшится. Подобно этому водяной поток в трубе тем больше, чем сильнее давление и чем меньше сопротивление, которое оказывает труба движению воды.
В популярной форме этот закон можно сформулировать следующим образом: чем выше напряжение при одном и том же сопротивлении, тем выше сила тока и в то же время чем выше сопротивление при одном и том же напряжении, тем ниже сила тока.
Чтобы выразить закон Ома математически наиболее просто, считают, что сопротивление проводника, в котором при напряжении 1 В проходит ток 1 А, равно 1 Ом.
Ток в амперах можно всегда определить, если разделить напряжение в вольтах на сопротивление в омах. Поэтому закон Ома для участка цепи записывается следующей формулой:
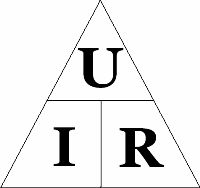
Любой участок или элемент электрической цепи можно охарактеризовать при помощи трёх характеристик: тока, напряжения и сопротивления.
Как использовать треугольник Ома: закрываем искомую величину – два других символа дадут формулу для её вычисления. Кстати, законом Ома называется только одна формула из треугольника – та, которая отражает зависимость тока от напряжения и сопротивления. Две другие формулы, хотя и являются её следствием, физического смысла не имеют.
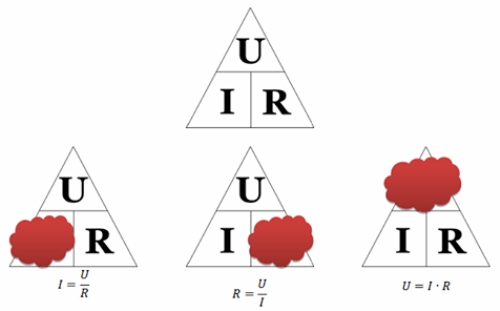
Расчеты, выполняемые с помощью закона Ома для участка цепи, будут правильны в том случае, когда напряжение выражено в вольтах, сопротивление в омах и ток в амперах. Если используются кратные единицы измерений этих величин (например, миллиампер, милливольт, мегаом и т. д.), то их следует перевести соответственно в амперы, вольты и омы. Чтобы подчеркнуть это, иногда формулу закона Ома для участка цепи пишут так:
Можно также рассчитывать ток в миллиамперах и микроамперах, при этом напряжение должно быть выражено в вольтах, а сопротивление — в килоомах и мегаомах соответственно.
Другие статьи про электричество в простом и доступном изложении:
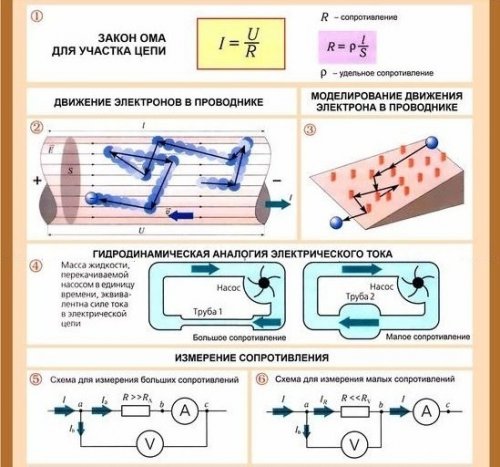
Закон Ома справедлив для любого участка цепи. Если требуется определить ток в данном участке цепи, то необходимо напряжение, действующее на этом участке (рис. 1), разделить на сопротивление именно этого участка.
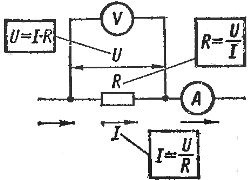
Рис 1. Применение закона Ома для участка цепи
Приведем пример расчета тока по закону Ома . Пусть требуется определить ток в лампе, имеющей сопротивление 2,5 Ом, если напряжение, приложенное к лампе, составляет 5 В. Разделив 5 В на 2,5 Ом, получим значение тока, равное 2 А. Во втором примере определим ток, который будет протекать под действием напряжения 500 В в цепи, сопротивление которой равно 0,5 МОм. Для этого выразим сопротивление в омах. Разделив 500 В на 500 000 Ом, найдем значение тока в цепи, которое равно 0,001 А или 1 мА.
Часто, зная ток и сопротивление, определяют с помощью закона Ома напряжение. Запишем формулу для определения напряжения
Из этой формулы видно, что напряжение на концах данного участка цепи прямо пропорционально току и сопротивлению . Смысл этой зависимости понять нетрудно. Если не изменять сопротивление участка цепи, то увеличить ток можно только путем увеличения напряжения. Значит при постоянном сопротивлении большему току соответствует большее напряжение. Если же надо получить один и тот же ток при различных сопротивлениях, то при большем сопротивлении должно быть соответственно большее напряжение.
Напряжение на участке цепи часто называют падением напряжения . Это нередко приводит к недоразумению. Многие думают, что падение напряжения есть какое-то потерянное ненужное напряжение. В действительности же понятия напряжение и падение напряжения равнозначны. Потери и падение напряжения – в чем различие?
Расчет напряжения с помощью закона Ома можно показать на следующем примере. Пусть через участок цепи с сопротивлением 10 кОм проходит ток 5 мА и требуется определить напряжение на этом участке.
Умножив I = 0,005 А на R —10 000 Ом, получим напряжение,равное 5 0 В. Можно было бы получить тот же результат, умножив 5 мА на 10 кОм: U = 50 В
В электронных устройствах ток обычно выражается в миллиамперах, а сопротивление — в килоомах. Поэтому удобно в расчетах по закону Ома применять именно эти единицы измерений.
По закону Ома рассчитывается также сопротивление, если известно напряжение и ток. Формула для этого случая пишется следующим образом: R = U/I.
Сопротивление всегда представляет собой отношение напряжения к току. Если напряжение увеличить или уменьшить в несколько раз, то ток увеличится или уменьшится в такое же число раз. Отношение напряжения к току, равное сопротивлению, остается неизменным.
Не следует понимать формулу для определения сопротивления в том смысле, что сопротивление данного проводника зависит оттока и напряжения. Известно, что оно зависит от длины, площади сечения и материала проводника. По внешнему виду формула для определения сопротивления напоминает формулу для расчета тока, но между ними имеется принципиальная разница.
Ток в данном участке цепи действительно зависит от напряжения и сопротивления и изменяется при их изменении. А сопротивление данного участка цепи является величиной постоянной, не зависящей от изменения напряжения и тока, но равной отношению этих величин.
Когда один и тот же ток проходит в двух участках цепи, а напряжения, приложенные к ним, различны, то ясно, что участок, к которому приложено большее напряжение, имеет соответственно большее сопротивление.
А если под действием одного и того же напряжения в двух разных участках цепи проходит различный ток, то меньший ток всегда будет на том участке, который имеет большее сопротивление. Все это вытекает из основной формулировки закона Ома для участка цепи, т. е. из того, что ток тем больше, чем больше напряжение и чем меньше сопротивление.
Расчет сопротивления с помощью закона Ома для участка цепи покажем на следующем примере. Пусть требуется найти сопротивление участка, через который при напряжении 40 В проходит ток 50 мА. Выразив ток в амперах, получим I = 0,05 А. Разделим 40 на 0,05 и найдем, что сопротивление составляет 800 Ом.
Закон Ома можно наглядно представить в виде так называемой вольт-амперной характеристики . Как известно, прямая пропорциональная зависимость между двумя величинами представляет собой прямую линию, проходящую через начало координат. Такую зависимость принято называть линейной .
На рис. 2 показан в качестве примера график закона Ома для участка цепи с сопротивлением 100 Ом. По горизонтальной оси отложено напряжение в вольтах, а по вертикальной оси — ток в амперах. Масштаб тока и напряжения может быть выбран каким угодно. Прямая линия проведена так, что для любой ее точки отношение напряжения к току равно 100 Ом. Например, если U = 50 В, то I = 0,5 А и R = 50 : 0,5 = 100 Ом.
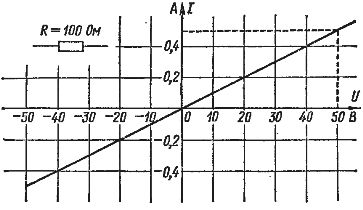
Рис. 2 . Закон Ома (вольт-амперная характеристика)
График закона Ома для отрицательных значений тока и напряжения имеет такой же вид. Это говорит о том, что ток в цепи проходит одинаково в обоих направлениях. Чем больше сопротивление, тем меньше получается ток при данном напряжении и тем более полого идет прямая.
Приборы, у которых вольт-амперная характеристика является прямой линией, проходящей через начало координат, т. е. сопротивление остается постоянным при изменении напряжения или тока, называются линейными приборами . Применяют также термины линейные цепи, линейные сопротивления.
Существуют также приборы, у которых сопротивление изменяется при изменении напряжения или тока. Тогда зависимость между током и напряжением выражается не по закону Ома, а более сложно. Для таких приборов вольт-амперная характеристика не будет прямой линией, проходящей через начало координат, а является либо кривой, либо ломаной линией. Эти приборы называются нелинейными .
ЭДС. Закон Ома для полной цепи
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е. против направления тока).
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1 ).

Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2 ).

Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение на резисторе .
За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:
Итак, , и мы приравниваем правые части формул (2) и (3) :
После сокращения на получаем:
Вот мы и нашли ток в цепи:
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4) ), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
Это напряжение является разностью потенциалов между точками и (рис. 2 ). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5) , что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3 и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).

Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло: .
Подставляем сюда выражения для , и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
или, что то же самое:
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .
Отметим два следствия выведенных формул (6) и (7) .
1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :
Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4 . Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
2. Закон Ома для участка и полной цепи
Закон Ома для участка цепи: сила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
Формула закона: I= . Отсюда запишем формулыU= IR и R =
. Отсюда запишем формулыU= IR и R = .
.
 Рис.1. Участок цепи
Рис.1. Участок цепи 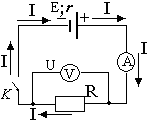 Рис.2. Полная цепь
Рис.2. Полная цепь
Закон Ома для полной цепи: сила тока I полной электрической цепи равна ЭДС (электродвижущей силе) источника тока Е, деленной на полное сопротивление цепи (R + r). Полное сопротивление цепи равно сумме сопротивлений внешней цепи R и внутреннего r источника тока. Формула закона I = 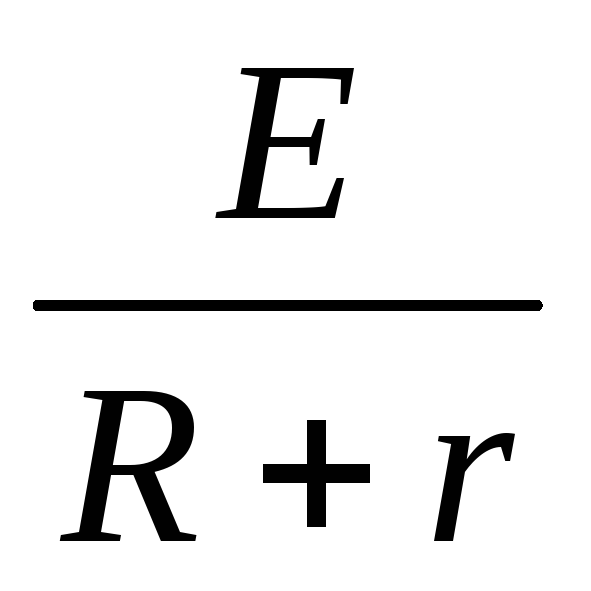 . На рис. 1 и 2 приведены схемы электрических цепей.
. На рис. 1 и 2 приведены схемы электрических цепей.
3. Последовательное и параллельное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно. Смешанное соединение сочетает оба эти соединения.
Сопротивление, при включении которого вместо всех других проводников, находящихся между двумя точками цепи, ток и напряжение остаются неизменными, называют эквивалентным сопротивлением этих проводников.
Последовательное соединение
Последовательным называется соединение, при котором каждый проводник соединяется только с одним предыдущим и одним последующим проводниками.
Как следует из первого правила Кирхгофа, при последовательном соединении проводников сила электрического тока, протекающего по всем проводникам, одинакова (на основании закона сохранения заряда).
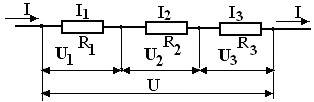 Рис. 1. Последовательное соединение двух проводников.
Рис. 1. Последовательное соединение двух проводников.
Напряжение при последовательном соединении проводников равно сумме напряжений на отдельных участках (проводниках) электрической цепи.
Этот результат справедлив для любого числа последовательно соединенных проводников.
Из закона Ома следует: при равенстве сил тока при последовательном соединении:
I = 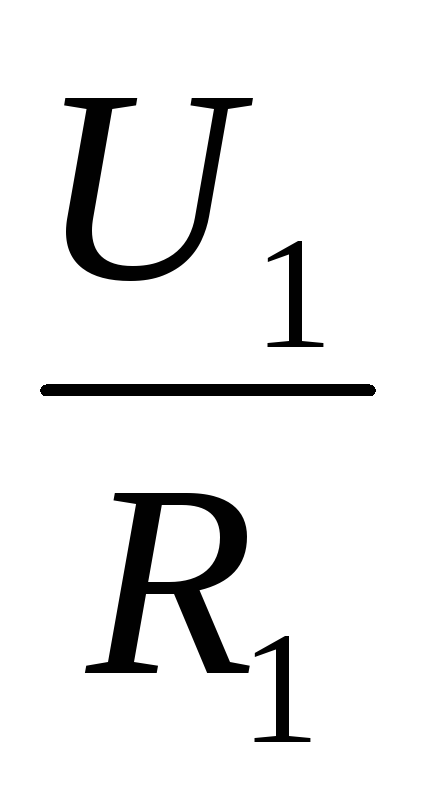 ,I =
,I =  . Отсюда
. Отсюда 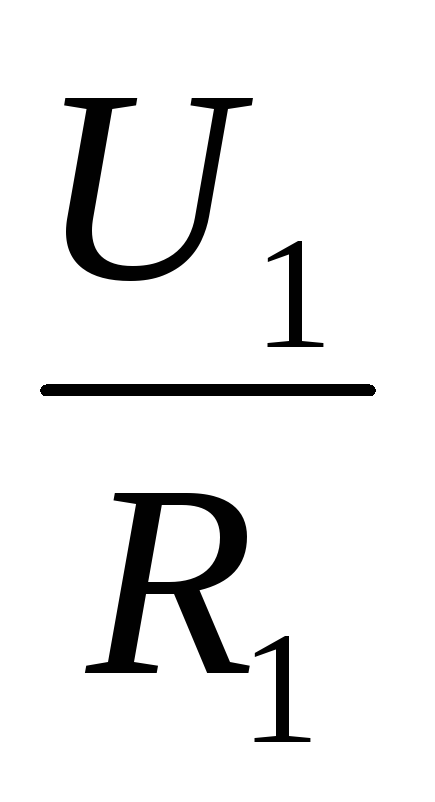 =
= 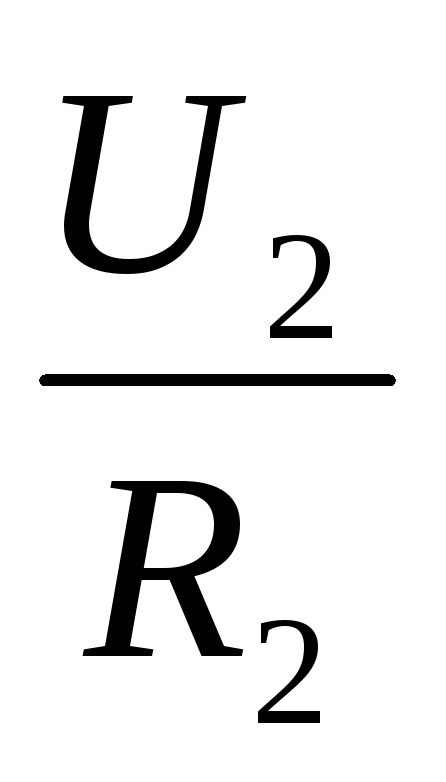 или
или 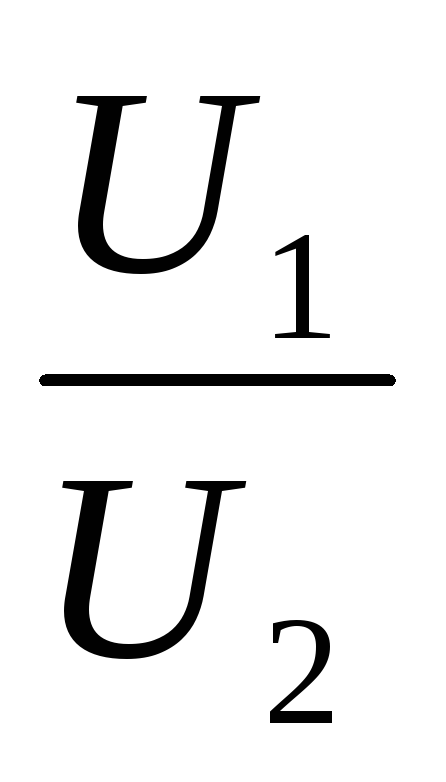 =
= , т. е. напряжения на отдельных участках цепи прямо пропорциональны сопротивлениям участков.
, т. е. напряжения на отдельных участках цепи прямо пропорциональны сопротивлениям участков.
При последовательном соединении n одинаковых проводников общее напряжение равно произведению напряжению одного U1 на их количество n:
При размыкании цепи одного из последовательно соединенных потребителей ток исчезает во всей цепи, поэтому последовательное соединение на практике не всегда удобно.

 ;
;
